Pythagorova a Euklidovy věty: Matematika na maturitě

Vítejte! Máme pro vás důležitou informaci ohledně matematiky na maturitě. Jestli vás zajímají Pythagorova a Euklidovy věty, nebo chcete zlepšit svoje znalosti matematiky, pak jste na správném místě. Pokračujte v čtení a objevte vše, co potřebujete vědět o těchto klíčových matematických pojmech.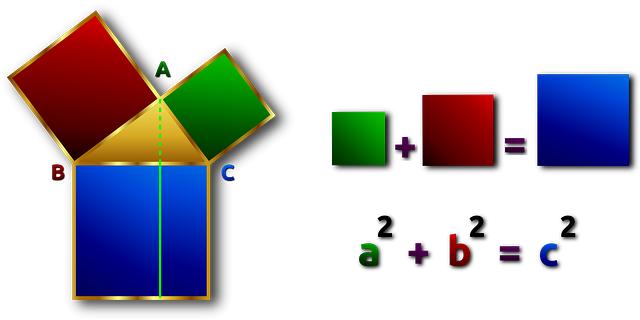
její význam a aplikace ve skutečném světě“>

Pythagorova věta: její význam a aplikace ve skutečném světě

Pythagorova věta je jedním z nejdůležitějších vztahů v geometrii a matematice jako celku. Tato věta nám říká, že ve trojúhelníku s pravým úhlem je druhá mocnina délky přepony rovná součtu druhých mocnin délek obou odvěsen. To má zásadní vliv na mnoho oblastí matematiky a její aplikace jsou velmi rozmanité.

Ve skutečném světě se Pythagorova věta využívá například v architektuře při výpočtech délek a úhlů ve stavebních plánech, v navigaci při stanovení vzdáleností mezi body na mapě nebo v technických oborech při výpočtech pravoúhlých trojúhelníků. Tato věta je jedním z kamenů základních matematických znalostí, které jsou důležité pro úspěch na maturitě.

Závěr

V článku jsme prošli základní principy a důležité věty Pythagora a Euklida, které mají v matematice zásadní význam. Znalost těchto vět je klíčová nejen pro úspěšné složení maturity, ale také pro pochopení matematických konceptů a aplikací v reálném světě. Doufáme, že vám tento článek poskytl užitečné informace a motivaci k dalšímu prozkoumávání matematiky. Pamatujte, že praktické použití matematiky je všude kolem nás, a tak je důležité ji nejen chápat, ale také se s ní aktivně angažovat. Vyjděte ze zkušeností Pythagora a Euklida a zkuste použít matematiku ve svém každodenním životě – možnosti jsou neomezené.