Kvadratická funkce: Matematika pro maturanty

Připravte se na jasný a zábavný průvodce matematickým světem kvadratických funkcí! Tento článek „Kvadratická funkce: Matematika pro maturanty“ vám odhalí všechny důležité informace, které potřebujete pro úspěšné zvládnutí tohoto důležitého matematického konceptu. Buďte připraveni na odemykání tajemství kvadratických funkcí s námi!

Úvod do kvadratických funkcí

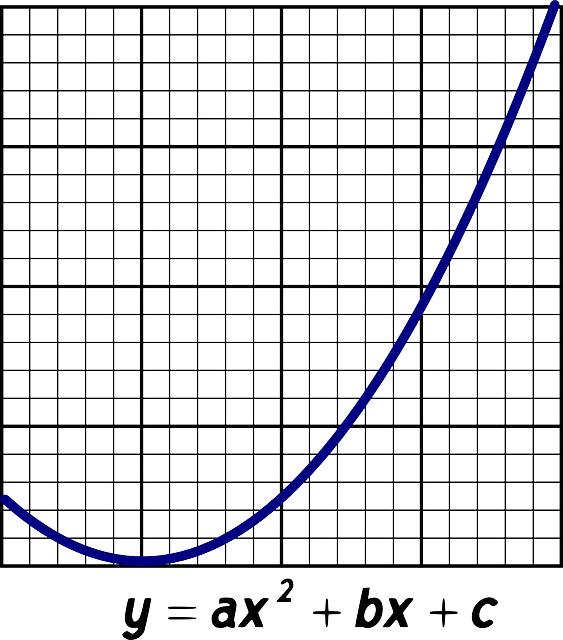
Pokud se chystáte na maturity z matematiky, jistě jste se již setkali s kvadratickými funkcemi. Tyto funkce jsou důležitou součástí učiva a je dobré je důkladně porozumět. Kvadratická funkce je matematická funkce, kterou lze zapsat ve tvaru y = ax² + bx + c, kde a, b a c jsou reálná čísla a a není rovno nule.

Význam kvadratických funkcí spočívá v tom, že se jedná o funkce, které mají parabolický tvar a často popisují různé jevy v reálném světě. Tyto funkce jsou také důležité pro pochopení základů algebry a matematické analýzy. Pochopení kvadratických funkcí vám proto pomůže nejen při zkouškách, ale i v dalším studiu matematiky a aplikací v životě.

Jednoduché kroky pro pochopení kvadratické funkce

Zde jsou některé jednoduché kroky, které vám pomohou lépe porozumět kvadratickým funkcím:

• Začněte seznámením se základními vlastnostmi kvadratické funkce, jako je tvar grafu a poloha vrcholu.
• Přezkoumejte si základní vzorec pro kvadratickou funkci: y = ax^2 + bx + c.
• Naučte se různé metody řešení kvadratických rovnic, jako je úplné čtverce nebo diskriminant.

Porozumění kvadratickým funkcím může být klíčové pro úspěšné absolvování maturity z matematiky. Sledujte náš blog, abyste získali další užitečné tipy a triky pro studium matematiky!

Výpočet kvadratických funkcí pomocí různých metod

Existuje několik způsobů, jak efektivně vypočítat kvadratické funkce v matematice. Mezi nejpoužívanější metody patří substituce, dokončení čtverce a kvadratická rovnice. Každá z těchto metod má své výhody a nevýhody, a je důležité znát, kdy a jak je použít.

Při použití substituce se kvadratická funkce převede na lineární rovnici, což usnadňuje další výpočty. Dokončení čtverce je také oblíbenou metodou, která umožňuje snadné nalezení řešení kvadratických funkcí. V neposlední řadě se kvadratické rovnice často řeší pomocí vzorců pro výpočet kořenů kvadratické funkce.

Praktické tipy pro efektivní řešení kvadratických rovnic

Pro efektivní řešení kvadratických rovnic je důležité mít pevné základy v matematice. Je nutné porozumět základním pravidlům a postupům, které nám pomohou vyřešit tyto rovnice rychle a přesně.

Zde jsou praktické tipy, které vám pomohou při řešení kvadratických rovnic:

• Dobře si rozmyslete, zda rovnice je kvadratická – Zamyslete se, zda má rovnice tvar ax^2 + bx + c = 0. Pokud ano, můžete ji zařadit mezi kvadratické rovnice.
• Použijte vhodnou metodu řešení – Existuje několik metod, jak kvadratickou rovnici vyřešit. Můžete využít například vzorec pro diskriminant nebo dokončení čtverce.
• Nezapomeňte ověřit vaše řešení – Po vyřešení rovnice je důležité ověřit správnost výsledku. Doporučuje se dosazení nalezených kořenů zpět do původní rovnice a jejich ověření.

Závěrečné myšlenky

V tomto článku jsme prozkoumali základní principy kvadratických funkcí a jejich využití v matematice. Doufáme, že jste získali hlubší porozumění tomuto konceptu a jeho aplikacím ve skutečném světě. Během studia matematiky je důležité mít pevný základ v kvadratických funkcích, protože se jedná o klíčovou část matematického učiva. Pokud si chcete rozšířit své znalosti v této oblasti, neváhejte hledat další informace a cvičení. Matematika může být skvělým způsobem, jak trénovat svou mysl a řešit složité problémy. Takže se pusťte do toho a zlepšte své matematické dovednosti!